Rozklady

Podstawowe informacje

Jeżeli

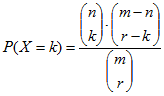
gdzie
to zmienna losowa X ma rozkład hipergeometryczny z parametrami m, n i r. Realizacje zmiennej losowej X można traktować jako liczbę wyróżnionych elementów w r-elementowej próbce, jeśli cała m-elementowa populacja zawiera n elementów wyróżnionych.

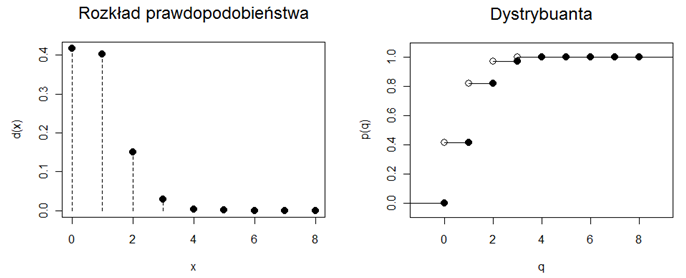
Rozkład prawdopodobieństwa i dystrybuanta
zmiennej losowej o rozkładzie hipergeometrycznym

Rozkład prawdopodobieństwa zmiennej losowej o rozkładzie hipergeometrycznym